My Run Expectancy Matrix
This past summer, I had the opportunity to work with the Spearfish Sasquatch Baseball Club, a collegiate summer ball team in the Expedition League based out of Spearfish, SD.
While working for the team, I was the official scorekeeper and statistician. Games were inputted through the software Pointstreak, which produced a variety of elementary statistics, but it lacked more modern player value stats.
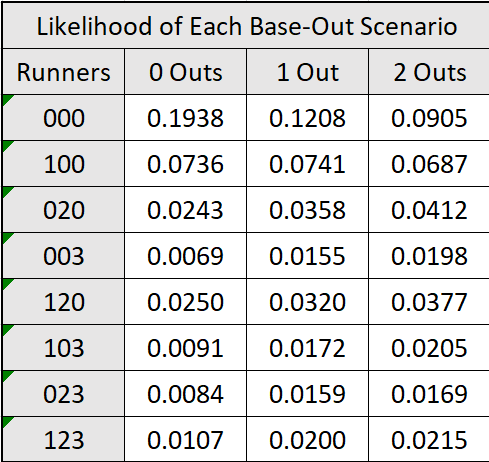
As a strong enthusiast of modern statistics, I tasked myself with calculating advanced metrics for the players on our roster and in the entire league. The first step to finding most advanced metrics is to create a Run Expectancy Matrix. This matrix has three columns and eight rows, comprising of the average run expectancy of each of the 24 base out scenarios. I logged data of every Sasquatch game throughout the season and inputted it all in Excel to create the following matrix:
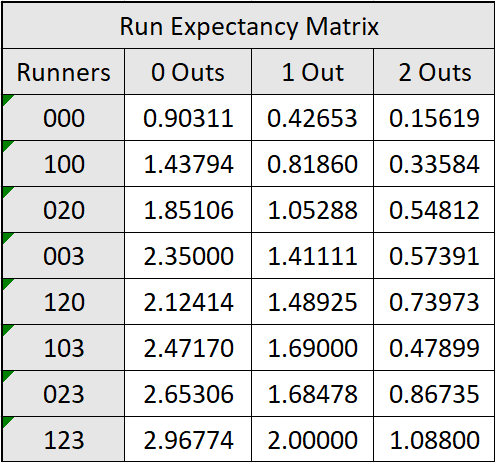
One thing I want to point out is that this matrix was created using only data from the 60 regular season Sasquatch games, rather than all 360 total regular season games played. This was for a few reasons, mainly because I watched every Sasquatch game and it would’ve taken much more time to create a matrix for the entire league. Because of this smaller and biased sample, the matrix may not accurately reflect the entire league, but I still think it tells us a lot about how baseball is played at this level. In this project, I will use this matrix, as well as similar ones from the EL and MLB to create a variety of fun and useful graphics.
Distribution Disparities
Overall, the matrix looks very practical. Generally, run expectancy increases as more runners reach base and decreases as outs increases. There are a few hiccups that may arise from a smaller sample size, such as how abnormally low the value at 2 Outs, Runners on first and third, or 2_103 abbreviated. Why might this be?
Here is a set of histograms displaying the distribution of each cell in the matrix, with the red dotted line denoting the average.
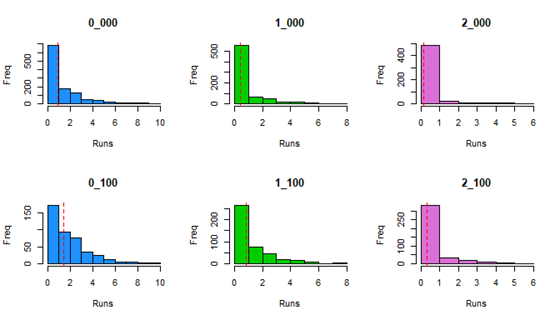
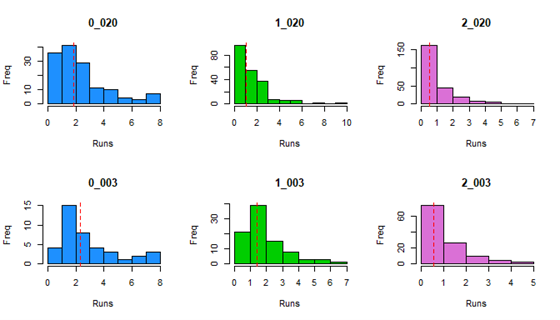
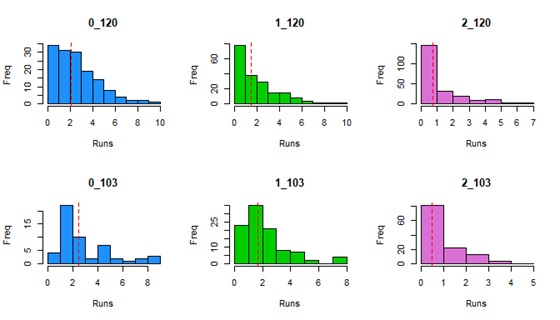
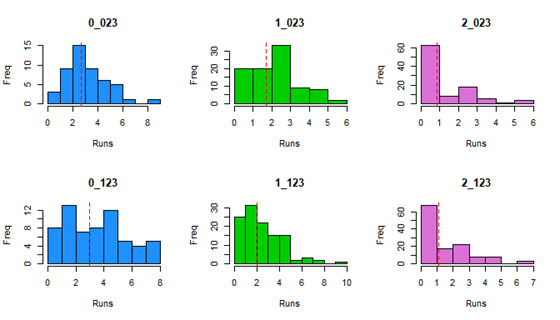
Most distributions look relatively normal, with a maximum around the average and a steep slope as values move farther away. Surely, with more data the distributions will look more and more normal. Does this explain why 2_103 is smaller than it should be? We see that the distribution is rather limited, and it actually has a max value of only 3.
We have seen the averages, but now let’s look at a series of boxplots to explore the median values and outliers.
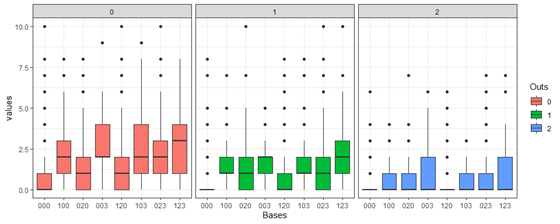
These boxplots match up pretty well with our histograms, showing us the distribution of each base-out state. Around the median is where most points are, with a few outliers. From this we see that the IQR of 2_103 is exactly that of 2_023 and is even greater than 2_120, but it is the possession of outliers that allow the latter to have a higher run expectancy than the former.
Expedition League vs. MLB
Run Expectancy
Now let’s look at a real Run Expectancy Matrix from MLB games. The most recent and updated matrix I was able to find on the internet is courtesy of Tom Tango, at this link. It has data from the years 2010-2015.
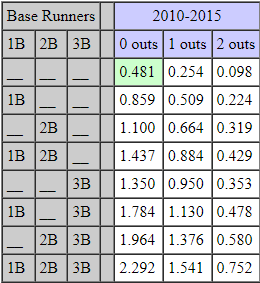
There may be discrepancies, as in the MLB during this time, teams averaged around 4.25 runs per game. Meanwhile, in Sasquatch games, teams scored an average of 7.57 runs per game.
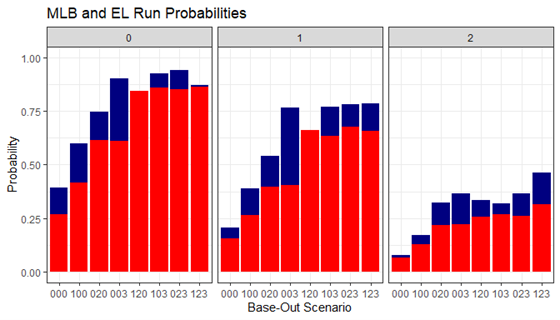
In these graphs, we see the different run expectancy for MLB and EL games, with Expedition League in Blue and MLB in Red.
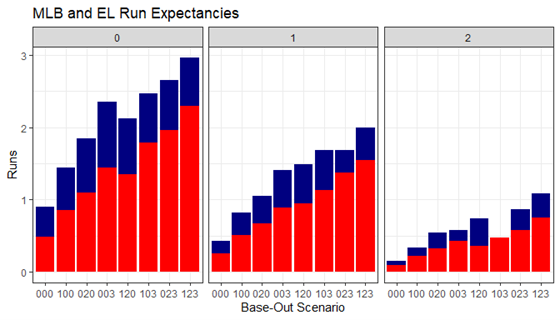
The graphs that we’re given tell us a story. With zero outs, the run expectancy of MLB and EL look very consistent, differing by a very similar amount each time. As the amount of outs increases, so does the inconsistency. With two outs, the overlaid bars look much different than they did in the first two graphs. In fact, at 2_103, the run expectancy in the MLB is actually higher than the EL, by a slim margin.
Run Probability
Tom Tango also provides us with a run probability matrix, displaying the probability of scoring a run at each base-out state. Here is our probability matrix, as well as Tango’s:
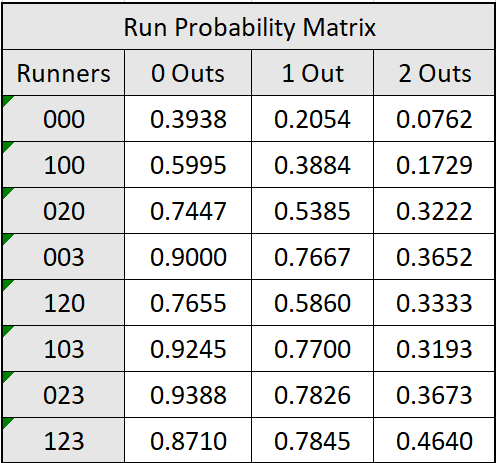
Let’s see how these two stack up against each other.
Something that surprised me is the difference between runners on first and second (120) and a runner on third (003) in the two leagues.
In the Expedition League, having a runner on third base makes a team just about as likely to score as runners on first and third, second and third, or bases loaded. This tells us that no matter how many runners are on base, as long as there is someone on third, the probability of scoring that inning remains the same.
In the MLB, this is not the case at all, as it is much more favorable to have runners on first and second.
This is likely due to the Expedition League’s high amount wild pitches, which allow the runner on third to score. In the MLB, this runner likely has to get batted in, which is more difficult.
Frequency of Each Base-Out State.
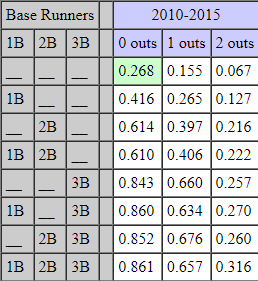
The final matrix that Tango provides tells us the frequency of each base-out state. This matrix has the percent of total instances that each base-out state represents.
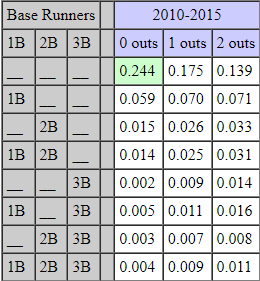
I also created one of these matrices for the Expedition League. Here are both of them:
Now let’s look at these probabilities in the form of a tree map.
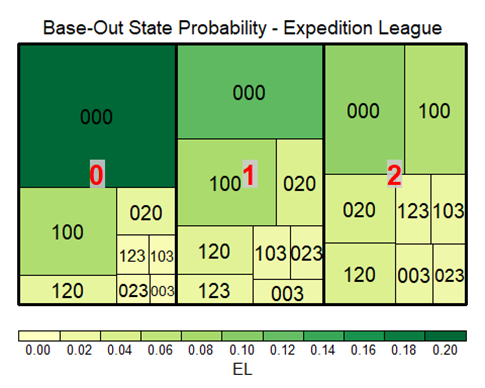
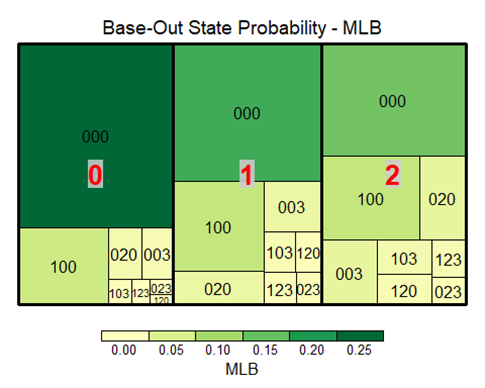
The first thing that jumps out at us is how frequently runners are on base in the Expedition League. The 000 boxes in the EL map are considerably smaller.
As it turns out, in the Expedition League runners are on base for 59.49% of all instances. In the MLB, this number is just 44.3%. This is consistent with what we’ve seen this whole time: The Expedition League is a much higher scoring league.
Linear Regression Model
How accurately can we predict my Expedition League Run Expectancy Matrix using data from our other matrices, both MLB and EL?
This is a fun way to see how these six total matrices compare with one other. How well can we predict one of them using the other five? Let’s see.
Using R’s lm() function and AIC, we find our best model to be:
y = -0.15756 + 0.91084x1 + 1.10894x2 + 1.19993x3 + e
with the following predictors:
MLB Run Expectancy = 0.91084
EL Run Probability = 1.10894
EL Base-Out Probability = 1.19993
MLB RE is our most significant predictor, with a p-value of 1.59e-07.
This model is highly effective, with an R2 of 0.9791, telling us that our model explains nearly 98% of all variation. Extremely effective.
Let’s look at the graph of predicted vs. actual values. The three points with the highest variation (≥ 0.175) are labeled.
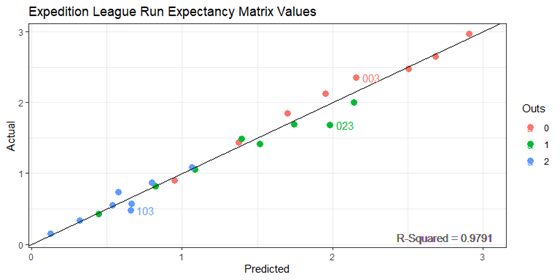
Overall, a fantastic fit.
Hey, there’s our old friend 2_103 again.