Situational Baseball
Since it’s conception, baseball has been a game heavily focused on strategy. Every pitch comes with a multitude of decisions, from split-second reactions to carefully crafted game plan.
Offensively, the name of the game is run production. It’s pretty simple: the team that scores the most, wins. However, getting runs on the board isn’t always flashy home runs or clutch singles; situational baseball can play a huge role in advancing runners and driving them home.
But, the game is changing. Now more than ever, teams are looking at advanced metrics and placing an emphasis on increasing launch angles and exit velocities. This new era has birthed soaring home run and strikeout rates, leaving traditional contact hitters in the dust. With the game of baseball looking much different than it did at the turn of the century, it makes us question whether traditional strategic methods still work, especially when looking at a league full of young, college kids.
I myself am a huge supporter of sabermetrics, and I believe these changes allow organizations to optimize player performance. However, as someone who has watched and been around baseball my entire life, I still greatly enjoy when teams play some small-ball in order to manufacture an important run.
After working with the Spearfish Sasquatch of the Expedition League this passed summer, I was able to create the perfect tool to answer these questions: a Run Expectancy Matrix. With this matrix, I can show just how many runs are gained or lost when teams play situational baseball.
Expedition League Matrices
A Run Expectancy Matrix is a table with 24 cells containing the expected amount of runs that will occur in an inning for each base-out scenario. A base-out scenario is the combination of outs and runners on base. For example, one out (1) and runners on first and second base (120) becomes the base-out state of 1_120. Here is the matrix from the Expedition League 2021.
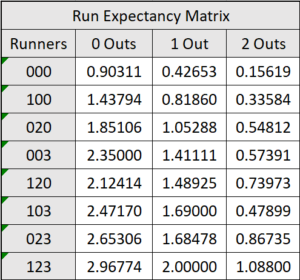
To see how this matrix stacks up to the MLB matrix, check out my Run Expectancy Matrix Project
This matrix will be used as our main tool for assessing how successful traditional baseball tactics truly are, on average.
However, sometimes in baseball you only need to score one run. With that in mind, it is also important to use a Run Probability Matrix, which will show us the probability of scoring at least one run from that base-out state.
Here is the matrix that I collected from the Expedition League:
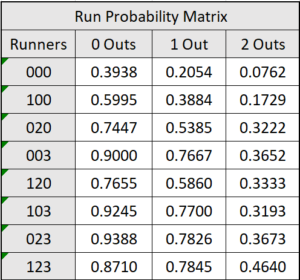
Now that we have established the matrices, let’s get into our analysis.
Stolen Bases
One of the most infamous strategic moves in baseball is the stolen base. It is an exciting play that almost always comes down to a split-second difference between safe and out. Players like Ricky Henderson and Tim Raines had long, Hall of Fame careers centered around swiping extra bases.
However, while stolen bases can help manufacture runs, getting caught stealing can wipe out an entire inning. There is a delicate trade off that coaches and players must be aware of in order to maximize run production.
Based on the matrices above, I calculated the trade off for each of the most common stolen base scenarios:
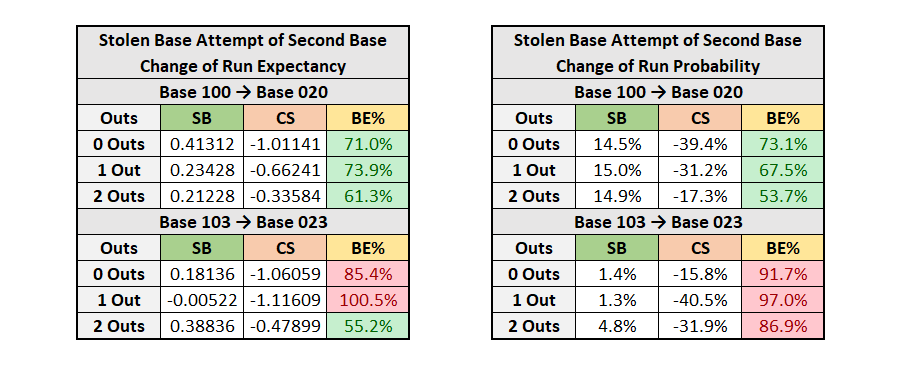
A few disclaimers: Expedition League data is not perfect. Statisticians for each team were sometimes untrustworthy and incorrect. Overwhelmingly, the data is correct, just not perfect. Also, data is unavailable separating steals of second base from steals of third base. In the real world, they have very different rates of success, which may slightly affect our rate for stealing second base.
I have columns denoting the change in run expectancy or probability based on whether the runner was safe or caught stealing.
In the final column, I have the break-even rate, which is the stolen base percentage that is required to reach net zero runs over time. This value is important to consider when deciding whether to send a runner to steal a base.
A manager must ask themselves: “Do I think the runner has an X% chance of being safe?”.
If the answer is yes, then on average it is the correct decision to send the runner. If no, then he should probably not attempt a steal, as it may cost the team runs.
In this case, I have conditionally formatted that column as such:
Green: Rate is below Expedition League SB% of 75.53%, have confidence sending the runner!
Red: Rate is above Expedition League SB% of 75.53%, hold at current base.
Of course, this is on average. A runner’s success rate varies greatly for each base runner, pitcher, catcher, count, etc.
I even made a team specific set of graphs for my Expedition League team, the Spearfish Sasquatch.
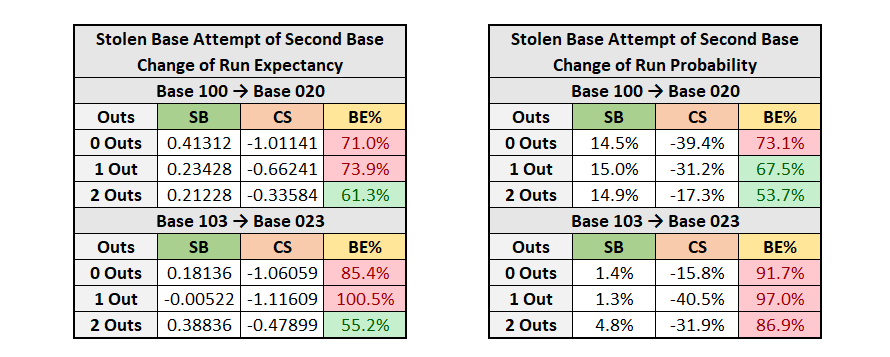
The cutoff rate here is a little bit different, as the Sasquatch had a below average SB% of 69.57%.
Looking at the data overall, we see a sharp contrast between our two scenarios. At the full EL rate, it is beneficial to steal second base with only a runner on first, as the rate eclipses the break-even rate of both expectancy and probability. However, it is not advised to steal second when there is already a runner on third, being thrown out can kill the chances of a big inning.
Now for the Sasquatch, things are a bit different. Unless there is an elite base-stealer on first, the only time I would advise stealing second base is when there are two outs and only a runner on first. In this case, a successful steal can put a runner in a great chance to score, while a caught stealing has little damage.
Even then, I would be slightly hesitant, as the Sasquatch boasted a league-best Extra-Base Hit Rate of 9.17%, making it more likely a runner can score from first without having to steal second.
Sacrifice Bunts
Ah, the sacrifice bunt. It is the quintessence of small-ball.
It is a strategy that has long been used in the process of run production: sacrificing an out in order to advance runners one base. It is also a strategy that is dying out in the era of sabermetrics, as more and more it is proven that giving up an out to advance a runner just isn’t worth it, especially with the home run rate rising annually.
However, it is still used frequently, mostly by pitchers, as for them swinging the bat can be more devastating than giving themselves up to advance a runner.
Let’s see how the sacrifice bunt fares in the Expedition League:
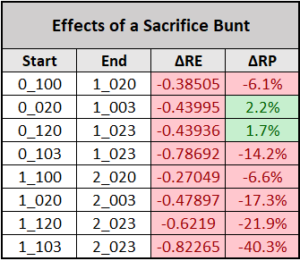
As we can see, not very well at all.
From a run expectancy standpoint, the sacrifice bunt is abysmal for the average hitter, taking away chunks of runs throughout a season.
However, there are two green cells in this graphic! Sacrifice bunts with a runners on first and second, or just second, and nobody out can increase a team’s chance of bringing a run home. The silver lining is it comes at the expense of around 0.44 runs off the board.
So is it worth it to even sacrifice with the average hitter? The answer is yes. And, surprisingly, it happens quite often.
For the COVID shortened 2020 MLB season, a new extra inning rule was implemented, where teams would start an inning with a runner already on second base. The Expedition League followed in MLB’s footsteps, using this rule in their 2021 campaign.
Extra innings by nature are sudden death. If one team scores more than the other in just one inning, they win the game. This is where sacrifice bunting and run probability comes into play. If a team finds themselves only needing one run in order to win, the smart play to begin the inning (Base-Out 0_020) is to bunt the runner over from second to third. Even if the defense is playing strategically and chooses to walk the first batter (0_120) the smart play remains the same: bunt the runner over.
As it turns out, a very non-traditional extra innings rule is what it takes to save the very traditional sacrifice bunt. The beauty of irony.
Suicide Squeeze
The soft-spoken sacrifice bunt has a wild, crazy cousin. This gutsy play is seldom spoken of but is one of baseball’s most exciting plays: The Suicide Squeeze.
In this play, the runner on third base takes off with the pitch, sprinting in what appears to be a steal of home plate. The batter then attempts to bunt the ball into the field of play. A successful bunt will bring the runner home before the defense has enough time to make the play, and they are forced to throw the batter out at first. An unsuccessful bunt hangs the lead runner out to dry in between third base and home plate.
This play holds a special place in my heart, as it is quite possibly my favorite baseball play. In my own baseball career, I was once tasked with laying the bunt down in a squeeze play. Laying the bunt down on that pitch was one of my most exhilarating and locked-in plate appearances I have had, but it was well worth it to see my runner safe at home.
There is a reason why this play is seldom used. It is extremely risky, and doesn’t fare too well on the side of run expectancy either.
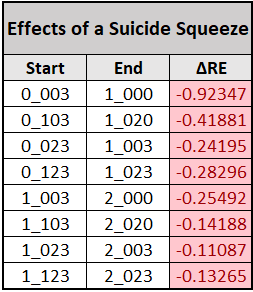
As we see in the table, even a successful suicide squeeze attempt is detrimental to run expectancy.
However, just like the sacrifice bunt, the suicide squeeze has its place in the game. After all, a successful squeeze attempt instantly jumps run probability to 100%. But with the danger of a failed attempt, at what point is it worth it?
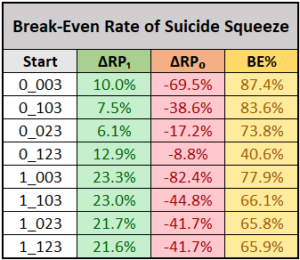
This table shows us the break-even points of the suicide squeeze in different base-out states. The green column shows us the change in run probability when a squeeze is perfectly executed. The red column shows us the change when it does the opposite, causing the runner on third to make an out.
The average break-even point is at 70.1%.
Generally, a manager needs to be extremely confident in his batter to lay the bunt down in order for the squeeze to be a productive play, on average. But if a team is ever in the need of only one run and can execute a suicide squeeze at least 70% of the time, they will succeed in scoring the run more often than a team that swings away.
So, are traditional strategic methods still effective?
Our triumphant answer is yes!
Well, at least sometimes…
Even in a league full of young ballplayers trying to stand out, traditional baseball methods can give a team the edge, when used correctly.
In the lofty world of launch angles and fly balls, it’s great to see that sometimes the best move is to play a little small ball.